The future value formula, given by
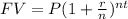
Can be used to obtain the Principal by substituting other values into the equation and solving for P
Step 1: List out the parameters given
FV =$8,700
r=7%=0.07
n=4 (since there are 4 quarters in a year)
t=6 (since it will be compounded 6 times a year)
Step 2: Substitute the values into the formula

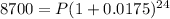
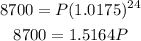
Solving for P
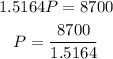
P=$5737.11
Option B is correct