Question

Find all X values where the tangent line to the graph of the function…

Answer 1

Consider the function,

`f(x)=6\sin x+(9)/(8)`

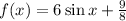
The first derivative gives the slope (m) of the tangent of the curve,

`\begin{gathered} m=f^(\prime)(x) \\ m=(d)/(dx)(6\sin x+(9)/(8)) \\ m=6\cos x+0 \\ m=6\cos x \end{gathered}`

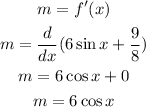
The equation of the line is given as,

`y-3\sqrt[]{3}x=(7)/(3)`

This can be written as,

`y=3\sqrt[]{3}x+(7)/(3)`

Comparing with the slope-intercept form of the equation of a line, it can be concluded that the given line has a slope,

`m^(\prime)=3\sqrt[]{3}`

Given that the tangent to the curve is parallel to this line, so their slopes must also be equal,

`\begin{gathered} m=m^(\prime) \\ 6\cos x=3\sqrt[]{3} \\ \cos x=\frac{\sqrt[]{3}}{2} \\ \cos x=\cos ((\pi)/(6)) \end{gathered}`

Consider the formula,

`\cos A=\cos B\Rightarrow A=2k\pi\pm B`

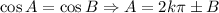
Applying the formula,

`x=2k\pi\pm(\pi)/(6)`

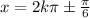
Thus, the required values of 'x' are,

`x=2k\pi\pm(\pi)/(6)`

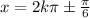
Therefore, options 1st and 2nd are the correct choices.