The triangle ΔDEF has the following coordinates
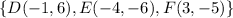
To find the area of a triangle in coordinate geometry, we have a formula. Given 3 vertices A(x1, y1), B(x2,y2) and C(x3,y3), the area of this triangle is given by
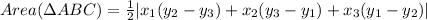
Using this formula for our problem, we have
![Area_(\Delta DEF)=(1)/(2)|(-1)((-6)-(-5))+(-4)((-5)-6)+3(6_{}-(-6))|]()
Solving this equation, we have
![\begin{gathered} Area_(\Delta DEF)=(1)/(2)|(-1)((-6)-(-5))+(-4)((-5)-6)+3(6_{}-(-6))| \\ =(1)/(2)|(-1)((-6+5)+(-4)(-5-6)+3(6_{}+6)| \\ =(1)/(2)|(-1)(-1)+(-4)(-11)+3(12)| \\ =(1)/(2)|1+44+36| \\ =(1)/(2)|81| \\ =(81)/(2) \\ =40.5 \end{gathered}]()
And this is our answer Area(ΔDEF) = 40.5