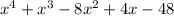Question

Given the zeros of the following polynomial 2 +2i, 3, - 4 select the corresponding factors AND the polynomia O (x + 2i) (2 - 2i) (2 - 3)(x+4) o f(c) = 24 - 23 822 - 42 - 48 0 (2 – 2i) (x + 2i) (2+3)(– 4) 24 – 13 + 82 40 - 48 0 (0 - 2) (+2)(x - 3)(x +4) 24 - 23 - 822 + 4x + 48 1 3 N

Answer 1

a)

d)

1) Since the zeros of that polynomial were given, then we can write it into the factored form. Note that there are 4 zeros, so we can write:

`\begin{gathered} (x-x_1)(x-x_2)(x-x_3)(x-x_4)=0 \\ (x-(-2i))(x-2i)(x-3)(x-(-4))=0 \\ (x+2i))(x-2i)(x-3)(x+4))=0 \end{gathered}`

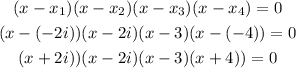
2) To find out the corresponding polynomial then we can expand it by rewriting "i" as -1

`\begin{gathered} (x+2i))(x-2i)(x-3)(x+4) \\ (x+2i)(x-2i)=x^2+4 \\ (x-3)(x+4)=x^2+4x-3x-12 \\ (x^2+4)(x^2+x-12) \\ x^4+x^3-8x^2+4x-48 \end{gathered}`

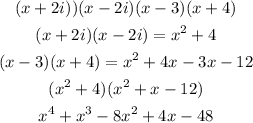
3) Hence, the answers are

a)

d)

`x^4+x^3-8x^2+4x-48`