Question

Find the ends of the major axisand foci.49x2 + 16y2 = 784Major axis (0,+[? ])

Answer 1

Major axis (0, +-14)

Step-by-step explanation:

The equation of an ellipse with the center in the origin is:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

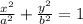
So, to transform the equation into this form, we need to divide both sides by 784 as:

`\begin{gathered} 49x^2+16y^2=784 \\ (49x^2)/(784)+(16y^2)/(784)=(784)/(784) \\ (x^2)/(16)+(y^2)/(49)=1 \end{gathered}`

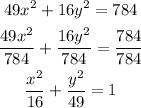
It means that a² = 16 and b² = 49. So, a = ±4 and b = ±7

Now, the major axis is 2 times the greater value between a and b. Since the greater value is b = 7, 2 times b is:

Major axis = (0, ±7*2) = (0, ±14)