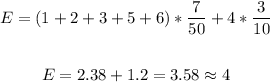The probablity of obtain a 4 is= 3/10
The probablity of obtain a 1,2,3,5,6,7,8= 1-3/10=7/10
The expect value is:
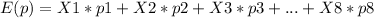
And p(1)=p(2)=p(3)=p(5)=p(6)=7/10
All have the same frequency, therefore
p(1,2,3,5,6,7,8)=7/10*1/5=7/50=1/10
Where x=1, 2 ,3,4,5,6 and p=3/10 if is 4 and 7/10 for any other number.
Replacing: