We know that two vectors are ortogonal if and only if:
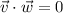
where
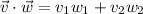
is the dot product between the vectors.
In this case we have the vectors:
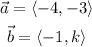
the dot product between them is:
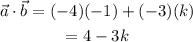
and we want them to be ortogonal, so we equate the dot product to zero and solve the equation for k:
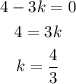
Therefore, for the two vector to be ortogonal k has to be 4/3.