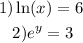
1) Let's rewrite it as a logarithmic expression of the following exponential one. Let's do it step by step.
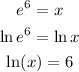
Note that when we apply the natural log on both sides, we use one of those properties that tell us that we can eliminate the log since the base of a natural log is "e", as well as, "e" is the base of that power.
2) To rewrite in the exponential form we can do the following:
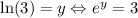
Note that in this case, we have used the definition of logarithms.