Question

In a certain country, the probability that a baby that is born is a boy is 0.52 and the probably that a baby that is born is a girl is 0.48. A family has two children. If X is the number of girls born to a family, find the probability that the family has 0, 1, or 2 girls.(a) Draw a tree diagram showing the possibilities for each outcome.(b) Create the binomial distribution table for p(X)

Answer 1

Given:

The probability that a baby that is born is a boy is 0.52.

The probability that a baby that is born is a girl is 0.48.

To find:

The probability that the family has 0, 1, or 2 girls.

Step-by-step explanation:

Using the binomial distribution,

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

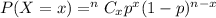
Here,

`\begin{gathered} n=2 \\ P(Birth\text{ of girls\rparen=}p=0.48 \\ P(B\imaginaryI rth\text{ of boys\rparen=}1-p=0.52 \end{gathered}`

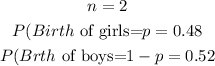
The probability that the family gets 0 girl child is,

`\begin{gathered} P(X=0)=^2C_0(0.48)^0(0.52)^2 \\ =0.2704 \end{gathered}`

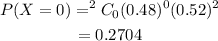
The probability that the family gets 1 girl child is,

`\begin{gathered} P(X=1)=^2C_1(0.48)^1(0.52)^1 \\ =0.2496 \end{gathered}`

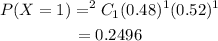
The probability that the family gets 2 girl children is,

`\begin{gathered} P(X=2)=^2C_2(0.48)^2(0.52)^0 \\ =0.2304 \end{gathered}`

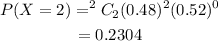
So, the probability that the family has 0, 1, or 2 girls is,

`\begin{gathered} P(E)=0.2704+0.2496+0.2304 \\ =0.7504 \end{gathered}`

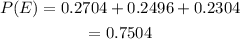
a) The tree diagram is,

b) The binomial distribution table for p(X) is,