Question

Freiese Um Which of the following is the graph of F(x) = 3x2 ?

Answer 1

To determine which is the graph of the function we can give some values to x to find point through the graph.

If x=0 then we have:

`\begin{gathered} F(0)=3(0)^2 \\ F(0)=0 \end{gathered}`

This means that the graph passes through the point (0,0).

If x=1 then we have:

`\begin{gathered} F(1)=3(1)^2 \\ F(1)=3(1) \\ F(1)=3 \end{gathered}`

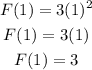
This means that the graph passes through the point (1,3)

If x=-1 then we have:

`\begin{gathered} F(-1)=3(-1)^2 \\ F(-1)=3(1) \\ F(-1)=3 \end{gathered}`

This means that the graph passes through the point (-1,3)

Hence we conclude that the graph has to pass through the points (0,0) (1,3) and (-1,3)

Looking at the graphs given we notice that the third graph fullfils these condition; therefore, the graph of the function is shown in option C