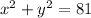Question

Writing the equation of a circle centered at the origin given it’s radius or appoint on the circle

Answer 1

The equation of the circle has the following form:

`(x-h)^2+(y-k)^2=r^2`

Where

(h,k) are the coordinates of the center of the circle

r is the radius of the circle

If the center of the circle is at the origin, (0,0) and it passes through the point (0,-9), since both x-coordinates are equal, the length of the radius is equal to the difference between the y-coordinates of the center and the given point:

`r=y_{\text{center}}-y_(point=)0-(-9)=0+9=9`

The radius is 9 units long.

Replace the coordinates of the center and the length of the radius in the formula:

`\begin{gathered} (x-0)^2+(y-0)^2=9^2 \\ x^2+y^2=81 \end{gathered}`

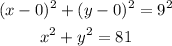
So, the equation of the circle that has a center in the origin and passes through the point (0.-9) is:

`x^2+y^2=81`