Question

Find the equations (in terms of x) of the line through the points (-2,-3) and (3,-5)

Answer 1

The general equation of a line passing through two points (xb₁,y₁)Pxb₂,y₂) is expressed as

`\begin{gathered} y-y_1=m(x-x_1) \\ \text{where} \\ m\Rightarrow slope\text{ of the line, expr}essed\text{ as }m\text{ = }(y_2-y_1)/(x_2-x_1) \\ (x_1,y_1)\Rightarrow coordinate_{}\text{ of point P} \\ (x_2,y_2)\Rightarrow coordinate_{}\text{ of point Q} \end{gathered}`

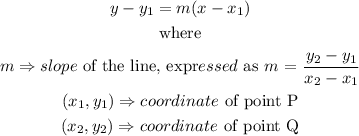
Given that the coordinates of the two points are (-2, -3) and (3, -5), we have

`\begin{gathered} (x_1,y_1)\Rightarrow(-2,\text{ -3)} \\ (x_2,y_2)\Rightarrow(3,\text{ -5)} \end{gathered}`

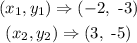
Step 1:

Evaluate the slope o the line.

The slope is thus evaluated as

`\begin{gathered} m\text{ = = }(y_2-y_1)/(x_2-x_1) \\ \text{ = }\frac{\text{-5-(-3)}}{3-(-2)} \\ =(-5+3)/(3+2) \\ \Rightarrow m\text{ = -}(2)/(5) \end{gathered}`

Step 2:

Substitute the values of x₁,

Thus, we have

`\begin{gathered} y-y_1=m(x-x_1) \\ x_1=-2 \\ y_1=-3 \\ m\text{ =- }(2)/(5) \\ \text{thus,} \\ y-(-3)\text{ = -}(2)/(5)(x-(-2)) \\ y+3\text{ =- }(2)/(5)(x+2) \end{gathered}`

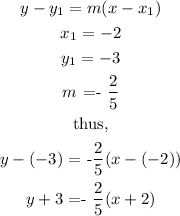
Step 3:

Make .

Hence, the equation of the line is

`y\text{ = -}(2)/(5)x\text{ - }(19)/(5)`

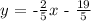
y₁ and m into the general equation of the line.