We are given a mid-point for segments AD and BC, we have the following:
segments AE and DE are congruent, that is:

By definition of mid-point.
Segments BE and CE are congruent, that is:

By definition of mid-point.
We also have that angles AEB and DEC are congruent, that is:
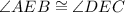
By the vertical angles theorem, which states that when two lines intercept their vertical or opposite angles are equal or congruent.
Now we can conclude that triangles AEB and DEC are congruent, that is:
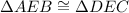
Due to the Side-Angle-Side Theorem, which states that when two triangles have two congruent sides and the angle between the congruent sides also congruent, then the triangles are congruent.