Question

This is lines , functions and systems. Graphing a line through a given point with a given slope.

Answer 1

The slope of the line is given as -2/3.

We are also given the point (1, 1) in which this line passes through.

Before we can plot the graph of the line, we need to know the equation of the line first.

The values given are more than enough to find the equation of the line.

The formula used to get the equation of the line is given below:

`\begin{gathered} m=(y-y_1)/(x-x_1) \\ \text{where,} \\ m=\text{slope} \\ _{} \\ x_1,y_1=\text{ The given point} \end{gathered}`

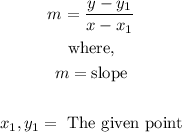
Now, with this formula, let us find the equation of the line.

`\begin{gathered} y_1=1,x_1=1,m=-(2)/(3) \\ m=(y-y_1)/(x-x_1) \\ \\ -(2)/(3)=(y-1)/(x-1)\text{ (Cross multiply)} \\ \\ -2*(x-1)=3(y-1) \\ -2x+2=3y-3 \\ \text{add 3 to both sides} \\ -2x+2+3=3y-3+3 \\ 3y=-2x+5 \end{gathered}`

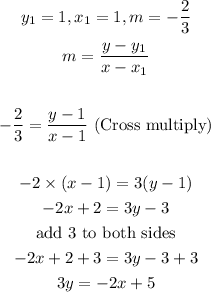
Thus, the equation of the line is:

`3y=-2x+5`

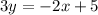
Now, using a graph calculator, let us plot this equation.

After doing this, the following is the result: