Let the number of hours be x,
Initial fee is $50,
Amount charged per hour is $8
The charge for a number of x hours is'
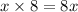
The total amount Esmeralda has is $150,
Therefore,
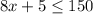
Solving for x to find the greates number of hours,

Hence, the greates number of hours is 12.5 hours.
Option B is the right answe