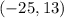Question

6. Point A is located at (7, -3) and point M is located at (-9,5). If M is themidpoint of segment AP, what are the coordinates of point P?"A) (-25, 13)B) (-1,1)C) (8,-4)OD) (25, -13)7 Name the ray that is opposite to ray CD."

Answer 1

The coordinates of P is;

`(-25,13)`

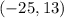
Step-by-step explanation:

Given that;

Point A is located at (7, -3) and point M is located at (-9,5).

And;

M is the midpoint of segment AP.

The coordinate of P will be represented by;

`P=(x_2,y_2)`

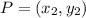
Using the formula for calculating midpoint;

`\begin{gathered} x=(x_1+x_2)/(2) \\ y=(y_1+y_2)/(2) \end{gathered}`

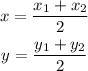
Making x2 and y2 the subject of formula;

`\begin{gathered} x_2=2x-x_1 \\ y_2=2y-y_1 \end{gathered}`

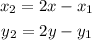
So, substituting the given coordinates;

`\begin{gathered} M=(x,y)=(-9,5) \\ A=(x_1,y_1)=(7,-3) \end{gathered}`

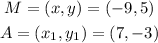
So, we have;

`\begin{gathered} x_2=2x-x_1 \\ x_2=2(-9)-7 \\ x_2=-25 \end{gathered}`

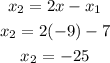
And;

`\begin{gathered} y_2=2y-y_1 \\ y_2=2(5)-(-3)=10+3 \\ y_2=13 \end{gathered}`

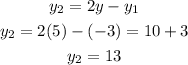
Therefore, the coordinates of P is;

`(-25,13)`