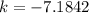Answer:
The value of k is;
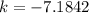
Step-by-step explanation:
Given the equation:
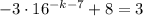
To solve, let us subtract 8 from both sides;
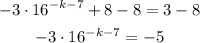
then, we can then divide both sides by -3;
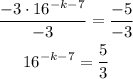
To solve further we need to take the logarithm of both sides;
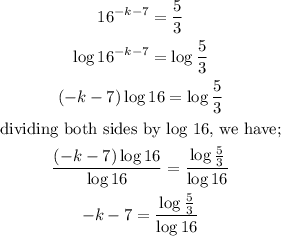
finding the value of the log;
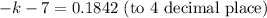
solving for k;
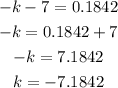
Therefore, the value of k is;