Question

QuestionGiven that cot(0)- 1 and 0 is in Quadrant II, what is sin(0)? Write your answer in exact form. Do not round.Provide your answer below:sin (O)=

Answer 1

Given:

The trigonometric ratio is given as,

`\cot \theta=-(1)/(2)`

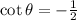
The value of θ lies in the second quadrant.

The objective is to find the value of sinθ.

Step-by-step explanation:

The formula of cotθ is,

`\cot \theta=\frac{\text{adjacent}}{\text{opposite}}=-(1)/(2)`

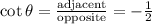
Since, the value of θ lies in second quadrant, the triangle formed for cotθ will be,

Then, the value of x can be calculated as,

`\begin{gathered} x^2=2^2+(-1)^2 \\ x=\sqrt[]{4+1} \\ x=\sqrt[]{5} \end{gathered}`

To find the value of sinθ:

The value of sinθ can be calculated as,

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \sin \theta=\frac{2}{\sqrt[]{5}} \\ \sin \theta=\frac{2}{\sqrt[]{5}}*\frac{\sqrt[]{5}}{\sqrt[]{5}} \\ \sin \theta=\frac{2\sqrt[]{5}}{5} \end{gathered}`

Hence, the value of sinθ is (2√5)/5.