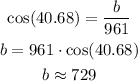Question

B 961 m Solve the triangle 40° 41 С b B= degrees minutes m (Round to the nearest whole number.) b = m (Round to the nearest whole number.)

Answer 1

To find the angle B we can use the propertie that sya that the sum of the internal angles of a triangle is equal to 180º so:

`\measuredangle b+90º+40º,41^(\prime)=180`

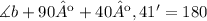
and we solve for angle b so:

`\begin{gathered} \measuredangle b=180º-90º-40º,41^(\prime) \\ \measuredangle b=49º,19^(\prime) \end{gathered}`

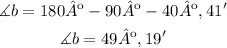
So B is equal to: 49 degrees and 19 minutes

So now to find a we can use the trigonometric identitie of sin so:

`\begin{gathered} \sin (40.68)=(a)/(961) \\ a=961\cdot\sin (40.68) \\ a\approx626 \end{gathered}`

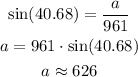
and to find b we use the trigonometryc identitie of cos so:

`\begin{gathered} \cos (40.68)=(b)/(961) \\ b=961\cdot\cos (40.68) \\ b\approx729 \end{gathered}`