Given that the operating voltage is V = 120 V.
The initial temperature of the toaster is T1 = 20 degrees Celsius
The initial current in the coil is I1 = 1.5 A
The final current in the coil is I2 = 1.3 A
The thermal coefficient of resistivity for nichrome is
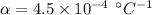
We have to find the final temperature of the coil, T2.
The initial resistance of the coil is

The final resistance of the coil is

The formula to calculate the final temperature of the coil is
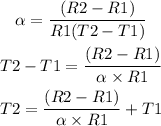
Substituting the values, the final temperature will be

Thus, the final temperature is 360 degrees Celsius.