General equation of an ellipse:
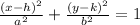
where (h,k) is the center, and a and b are some constants.
If b² is greater than a², then the y-axis is the major axis.
In this case, the ellipse is defined by the next equation:
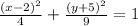
This means that:
![\begin{gathered} b^2=9 \\ b=\sqrt[]{9} \\ b=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pw76fw8cbsr2a30tjefin5nyi7ryqnj346.png)
And, h = 2, k = -5
The vertices on the major axis are computed as follows:
(h, k+b) and (h, k-b)
Substituting with h = 2, k = -5, and b = 3, the vertices are:
(2, -5+3) and (2, -5-3)
(2, -2) and (2, -8)