Answer
θ = 37° 30'
Step-by-step explanation:
The angle of depression has the same measure as the angle of elevation, so a trigonometric function that related the sides of the triangle and the angle of elevation θ is tangent. Then:
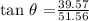
Therefore, the value of θ is:
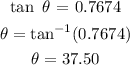
So, in grades and minutes, we get:
θ = 37.50 = 37° 30'
Therefore, the angle of depression is 37° 30'