Question

Moments after making the dreaded decision to jump out the door of the airplane, Darin's 75.5-kg body experiences +128 N of air resistance upward. Determine Darin's acceleration (in m/s^2) at this instant in time.Hint: Your answer will be negative since he is falling (i.e., his acceleration is still in the down direction). Answer: ________ m/s^2

Answer 1

Given:

The mass of the Darin is m = 75.5 kg

The air resistance is

`F_a=128\text{ N}`

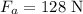
Required: Darin's acceleration.

Step-by-step explanation:

According to Newton's second law, the downward force will be

`F_g=\text{ mg}`

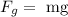
Here, g = -9.8 m/s^2 is the acceleration due to gravity.

On substituting the values, the downward force will be

`\begin{gathered} F_g=75.5*(-9.8) \\ =\text{ -739.9 N} \end{gathered}`

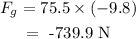
The net force will be

`\begin{gathered} F_(net)=\text{ F}_g+F_a \\ =-739.9+128 \\ =-611.9\text{ N} \end{gathered}`

Final Answer: Darin's acceleration is -611.9 N