To find:
The area of the training field.
Solution:
The training field is made of two semicircles and a rectangle.
The length and width of the rectangle is 96 m and 64 m. So, the area of the rectangle is:
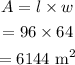
The diameter of the semicircle is 64 m. SO, the radius of the semicircle is 32 m.
The area of two semicircles is:
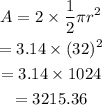
So, the area of the training field is:
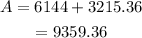
Thus, the area of the training field is 9359.36 m^2.