To determine the amount that will be on the account after 4 years you have to apply the given exponential function that models the amount of money on the account with respect to the time.
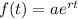
Where
a represents the initial amount
r represents the interest rate expressed as a decimal value
t is the time period in years
The initial amount on the account is a= $600
The time period is t= 4 years
The interest rate is r=5%, divide it by 100 to express it as a decimal value:
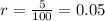
Using this information, you can calculate the final amount:
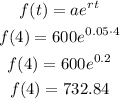
After 4 years there will be $732.84 on the account. The correct option is B.