SOLUTION:
Step 1:
In this question, we are given the following:
A circular pool measures 12 feet across.
One cubic yard of concrete is to be used to create a circular border of uniform width around the pool.
If the border is to have a depth of 6 inches, how wide will the border be?
Step 2:
From the question, we can see that:
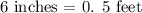
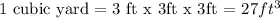

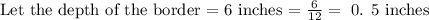
Step 3:
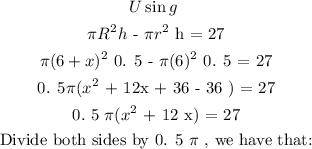
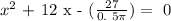
Solving this, we have that:
CONCLUSION:
From the calculations above, we can see that the value of the x:
( which is the width of the border ) = 1. 293 feet
(correct to 3 decimal places)