Given:
The system of equation is given as,
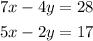
The objective is identify the augmented matrix for the system of equations and the solution using row operations.
Step-by-step explanation:
The required augmented matrix will be,
Performing the Gauss-Jordan elimination with the following operation,
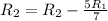
By applying the operation to the augmented matrix,
To find y :
On equating the second row of the matrix,
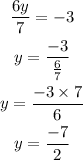
To find x :
On equating the first row of the matrix,
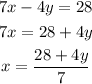
Substitute the value of y in the above equation.
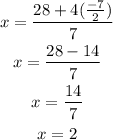
Thus the value of solutions are,
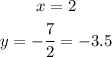
Hence, option (3) is the correct answer.