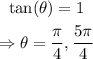Question

Use inverse trigonometric functions to solve the following equations. If there is more than one solution, enter all solutions as a comma-separated list (like "1, 3"). If an equation has no solutions, enter "DNE".Solve tan(θ)=1 for θ (where 0≤θ<2π).θ=Solve 7tan(θ)=−15 for θ (where 0≤θ<2π).θ=

Answer 1

Starting with the equation:

`\tan (\theta)=1`

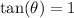
take the inverse tangent function to both sides of the equation:

`\begin{gathered} \arctan (\tan (\theta))=\arctan (1) \\ \Rightarrow\theta=\arctan (1) \\ \therefore\theta=(\pi)/(4) \end{gathered}`

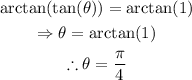
Yet another value can be found for this equation to be true since the period of the tangent function is π:

`\begin{gathered} \theta_1=(\pi)/(4) \\ \theta_2=(\pi)/(4)+\pi=(5)/(4)\pi \end{gathered}`

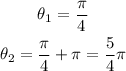
Starting with the equation:

`7\tan (\theta)=-15`

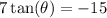
Divide both sides by 7:

`\Rightarrow\tan (\theta)=-(15)/(7)`

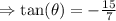
Take the inverse tangent to both sides of the equation:

`\begin{gathered} \Rightarrow\arctan (\tan (\theta))=\arctan (-(15)/(7)) \\ \Rightarrow\theta=\arctan (-(15)/(7)) \\ \therefore\theta=-1.13416917\ldots \end{gathered}`

The tangent function has a period of π. Since the value that we found for theta is not between 0 and 2π, then we can add π to the value:

`\begin{gathered} \theta_1=-1.13416917\ldots+\pi \\ =2.007423487\ldots \end{gathered}`

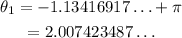
We can find another value for theta such that its tangent is equal to -15/7 by adding π again, provided that the result is less than 2π:

`\begin{gathered} \theta_2=\theta_1+\pi \\ =5.14901614\ldots \end{gathered}`

Therefore, for each equation we know that:

`\begin{gathered} \tan (\theta)=1 \\ \Rightarrow\theta=(\pi)/(4),(5\pi)/(4) \end{gathered}`
`\begin{gathered} 7\tan (\theta)=-15 \\ \Rightarrow\theta=2.007423487\ldots\text{ , }5.14901614\ldots \end{gathered}`