First, rewrite all the mixed fractions as impropper fractions:
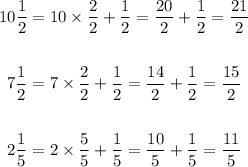
Next, multiply the rate of chocolate production over time by the the operating time of the machines to find the total amount of pounds of chocolate frogs produced in one day:
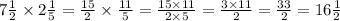
Then, the chocolate factory can produce 16 1/2 pounds of chocolate frogs per day.
Since 16 1/2 is greater than 10 1/2, then the chocolate factory will meet their goal with the total being over 10 1/2 pounds of chocolate frogs produced.