Question

A committee must be formed with 5 teachers and 4 students. If there are 6 teachers to choose from, and 15 students, how many different ways could the committee be made?

Answer 1

There are 6 teachers and 15 students to choose from

To form a committee of 5 teachers and 4 students

The combination rule will be applied

From 6 teachers, The number of ways 5 teachers can be selected is

`^6C_5`

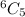
From 15 students, the number of ways 4 students can be selected is

`^(15)C_{4^{}}`

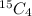
Therefore, the total number of ways a committee of 5 teachers and 4 students can be formed from 6 teachers and 15 students is

`^6C_5*^(15)C_{4^{}}`

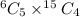
Simplifying this gives

`^6C_5*^(15)C_{4^{}}=(6!)/((6-5)!*5!)*(15!)/((15-4)!*4!)`

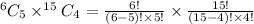
This further gives

`\begin{gathered} ^6C_5*^(15)C_{4^{}}=(6!)/(1!*5!)*(15!)/(11!*4!) \\ ^6C_5*^(15)C_{4^{}}=(6*5!)/(1*5!)*(15*14*13*12*11!)/(11!*4*3*2*1) \end{gathered}`

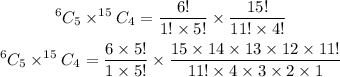
Cancel out common factors

`\begin{gathered} ^6C_5*^(15)C_{4^{}}=6*(15*14*13*12)/(4*3*2*1) \\ ^6C_5*^(15)C_{4^{}}=6*(32760)/(24) \\ ^6C_5*^(15)C_{4^{}}=6*1365 \\ ^6C_5*^(15)C_{4^{}}=8190 \end{gathered}`

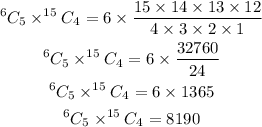
Therefore, the number of ways the committee can be formed is 8190 ways