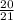Question

Need help pleaseI was bad at math in school so lwant to learn

Answer 1

The probability of an event is expressed as

`Pr(\text{event) =}\frac{Total\text{ number of favourable/desired outcome}}{Tota\text{l number of possible outcome}}`

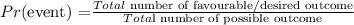
Given:

`\begin{gathered} \text{Red}\Rightarrow2 \\ \text{Green}\Rightarrow3 \\ \text{Blue}\Rightarrow2 \\ \Rightarrow Total\text{ number of balls = 2+3+2=7 balls} \end{gathered}`

The probability of drwing two blue balls one after the other is expressed as

`Pr(\text{blue)}* Pr(blue)`

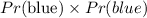
For the first draw:

`\begin{gathered} Pr(\text{blue) = }\frac{number\text{ of blue balls}}{total\text{ number of balls}} \\ =(2)/(7) \end{gathered}`

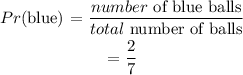
For the second draw, we have only 1 blue ball left out of a total of 6 balls (since a blue ball with drawn earlier).

Thus,

`\begin{gathered} Pr(\text{blue)}=\frac{number\text{ of blue balls left}}{total\text{ number of balls left}} \\ =(1)/(6) \end{gathered}`

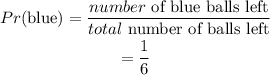
The probability of drawing two blue balls one after the other is evaluted as

`\begin{gathered} (1)/(6)*(2)/(7) \\ =(1)/(21) \end{gathered}`

The probablity that none of the balls drawn is blue is evaluted as

`\begin{gathered} 1-(1)/(21) \\ =(20)/(21) \end{gathered}`

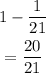
Hence, the probablity that none of the balls drawn is blue is evaluted as

`(20)/(21)`