Question

Please help me work through this, thank you! it specifies to round to 2 decimal places

Answer 1

Since they will collide the time taken for both to reach the intersection is the same.

Let the time taken by t.

Recall that for steady motion,

`\begin{gathered} d=st \\ \text{ Where:} \\ d=\text{ the distance covered} \\ s=\text{ the speed} \\ t=\text{ the time} \end{gathered}`

Substitute d = 4 and s = 442 into the equation:

`\begin{gathered} 4=442t \\ \text{ Dividing both sides by }442,\text{ it follows that:} \\ t=(4)/(442) \end{gathered}`

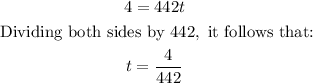
Therefore, the distance covered by the Coyote in this time is given by:

`d=(4)/(442)*481=(74)/(17)`

Using the Pythagorean Rule, it follows that the distance between Road Runner and the Coyote along the diagonal is given by:

`h=\sqrt{((74)/(17))^2+4^2}`

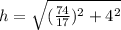
Since speed s for a body that travelled distance d in time t is given by:

`s=(d)/(t)`

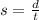
it follows that the required speed is given by:

`-\sqrt{((74)/(17))^2+4^2}*(442)/(4)=-65√(101)`

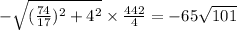
Therefore, the required rate is -65√101 kph.