Given Data:
The upstream speed is, 25 miles/hr.
The downstream speed is, 35 miles/hr.
The total time is, 12 hr.
Let d be the distance traveled. He can travel 25 miles/ hr in upstream, so the time taken will be,
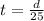
He can travel 35 miles/ hr in upstream, so the time taken will be,
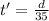
Total time is, 12 hr. So we have,
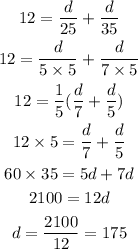
Therefore the total distance is, 350 mile