Let's call C to the cups of chocolate chips and S to the cups of sugar. We are told that the cups of sugar are 2 2/3 times the cups of chocolate, then we can formulate the following equation:
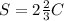
In the case 4 1/3 of sugar is added, we can replace 4 1/3 for S to get:
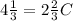
By dividing both sides by 2 2/3 we get:
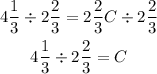
We can rewrite the mixed fractions to get:
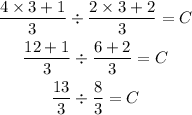
By changing the division symbol to a multiplication symbol and flipping the 8/3, we get:
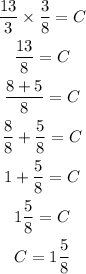
Then, 1 5/8 cups of chocolate chips are needed