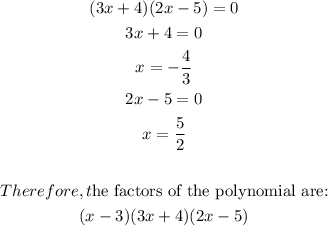Question

8. Factor ()=63−252++60 completely given that x=3 is a zero of p(x). Use only the techniques from the lecture on 3.3 (synthetic division). Other methods will receive a score of zero. Be sure to show all your work (including the synthetic division).

Answer 1

Factor the polynomial

`\begin{gathered} p(x)=6x^3-25x^2+x+60 \\ \text{Given that, }x=3\text{ is a zero} \end{gathered}`

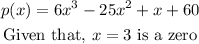
Using the synthetic division method to factorize the polynomial completely,

The resulting coefficients from the table are 6, -7, -20, 0

Thus the quotient is

`6x^2-7x-20`

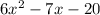
Factorizing the quotient completely,

`\begin{gathered} 6x^2-7x-20 \\ =6x^2-15x+8x-20 \\ =3x(2x-5)+4(2x-5) \\ =(3x+4)(2x-5) \end{gathered}`

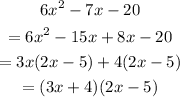
Therefore, the other two zeros of the polynomial are:

`\begin{gathered} (3x+4)(2x-5)=0 \\ 3x+4=0 \\ x=-(4)/(3) \\ 2x-5=0 \\ x=(5)/(2) \\ \\ Therefore,t\text{he factors of the polynomial are:} \\ (x-3)(3x+4)(2x-5) \end{gathered}`