Question

True or false the surface area of a sphere with a radius of 10 units is larger than the surface area of a cube with edge lengths of 10 units

Answer 1

The surface area of a sphere is given by

`S_s=4\pi r^2`

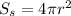
in our case r=10 units ( the radius). By substituting this value into the last formula, we have

`S_s=4(3.1416)(10^2)`

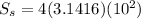
which gives

`S_s=1256.64u^2`

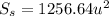
On the other hand, the surface area of a cube is given by

`S_c=6L^2`

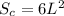
where L is the length of one side, that is, L=10. Then, we have

`\begin{gathered} S_c=6\cdot(10^2) \\ S_c=6\cdot100=600u^2 \\ S_c=600u^2 \end{gathered}`

By comparing both results, we can see that the surface area of our sphere is larger than the surface area of the given cube. So the answer is TRUE.