Question

| 5-6x | -12 = 0Solve the absolute. equation for 2 values of x

Answer 1

Given

`|5-6x|-12=0`

To solve this equation for both possible values of x, you have to separate it into two calculations.

1) One will be for the case that the values inside the absolute term are multiplied by "+1":

`\begin{gathered} 1\cdot(5-6x)-12=0 \\ 5-6x-12=0 \\ -6x+5-12=0 \\ -6x-7=0 \\ -6x=7 \\ -(6x)/(-6)=(7)/(-6) \\ x=-(7)/(6) \end{gathered}`

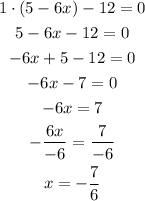
The first value of x is -7/6

2) The second will be the case that the absolute values are negative, that is as if they are multiplied by -1

`\begin{gathered} (-1)(5-6x)-12=0 \\ -5+6x-12=0 \\ 6x-5-12=0 \\ 6x-17=0 \\ 6x=17 \\ (6x)/(6)=(17)/(6) \\ x=(17)/(6) \end{gathered}`

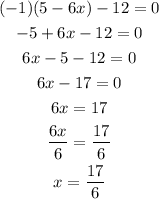
The second value of x is 17/6

So for this absolute equation, the possible values of x are -7/6 and 17/6