Question

Drag each label to the correct location on the table. Match each equation with its number of unique solutions. y = -52 – 41 +7 y = –202 + 91 - 11 y = 3.12 – 61 + 3 Two Real Solutions One Real Solution One Complex Solution Two Complex Solutions Reset Next reserved

Answer 1

When b²−4ac=0 there is one real root.

When b²−4ac>0 there are two real roots.

When b²−4ac<0 no real roots or two complex roots

First equation

-x²-4x+7

`\begin{gathered} b^(2)-4ac \\ \mleft(-4\mright)^2-4\mleft(-1\mright)\cdot\: 7 \\ 16+28=44 \end{gathered}`

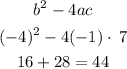
b²−4ac>0, then equation -x²-4x+7 has two real roots.

Second equation

-2x²+9x-11

`\begin{gathered} b^(2)-4ac \\ 9^2-4\mleft(-2\mright)\mleft(-11\mright) \\ 81-88=-7 \end{gathered}`

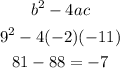
b²−4ac<0, then equation -2x²+9x-11 has two complex roots.

`x1=(9)/(4)-i(√(7))/(4),\: x2=(9)/(4)+i(√(7))/(4)`

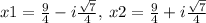
Third equation

3x²-6x+3

`\begin{gathered} b^(2)-4ac \\ \mleft(-6\mright)^2-4\cdot\: \: 3\cdot\: \: 3 \\ 36-36=0 \end{gathered}`

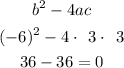
b²−4ac=0, then equation 3x²-6x+3 has one root.