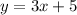Question

Find the equation of the line that is parallel to y= 3x -2 and contains the point (2,11) Y= ?x + ?

Answer 1

Given:

`\begin{gathered} y=3x-2 \\ \text{Through the point (2,11)} \end{gathered}`

Two parallel lines have identical slopes.

`m_1=m_2`

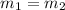
Hence, the slope of line 1 is gotten by comparing the equation given to the equation of a line in the slope-intercept form.

`\begin{gathered} y=mx+b \\ \text{where m is the slope} \\ b\text{ is the y-intercept} \end{gathered}`

Thus,

`\begin{gathered} y=mx+b \\ y=3x-2 \\ \\ \text{Comparing both equations,} \\ m_1=3 \\ \text{The slope of line 1 is 3.} \end{gathered}`

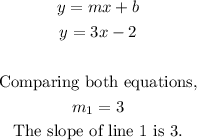
Since both lines are parallel, then the slopes are equal.

`\begin{gathered} m_1=m_2=3 \\ m_2=3 \\ \text{The slope of line 2 is 3} \end{gathered}`

To get the equation of line 2 through the point (2,11), the formula below is used;

`\begin{gathered} (y-y_1)/(x-x_1)=m \\ \\ \text{where;} \\ x_1=2 \\ y_1=11 \\ m=3 \\ \text{Hence,} \\ (y-11)/(x-2)=3 \\ \text{Cross multiplying,} \\ y-11=3(x-2) \\ y-11=3x-6 \\ y=3x-6+11 \\ y=3x+5 \end{gathered}`

Therefore, the equation of the line that is parallel to y = 3x - 2 passing through the point (2,11) is;

`y=3x+5`