Question

Tom said that the difference in length between the longest trail and the shortest trail is 2 5/8 miles. Does Tom's answer make sense? What mistake did he make? Answer in at least two complete sentences. Use the sentences below to get started: "Tom's answer (makes sense/does not make sense). His mistake was ________."

Answer 1

Given:

From the trail lengths given,

`\begin{gathered} The\text{ longest trail is }1(7)/(8) \\ The\text{ shortest trail is }(3)/(4) \end{gathered}`

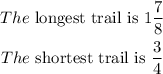
The difference in length between the longest trail and the shortest trail:

`\begin{gathered} 1(7)/(8)-(3)/(4)=(15)/(8)-(3)/(4) \\ =(15-6)/(8) \\ =(9)/(8) \\ =1(1)/(8) \end{gathered}`

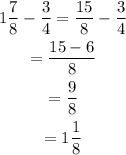
The sum of the longest trail and the shortest trail.

`\begin{gathered} 1(7)/(8)+(3)/(4)=(15)/(8)+(3)/(4) \\ =(15+6)/(8) \\ =(21)/(8) \\ =2(5)/(8) \end{gathered}`

From the calculations above, the conclusion can be reached that:

Tom's answer does not make sense. His mistake was he did the sum of the longest trail and the shortest trail.