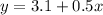Question

Find the slope, if it exists, of the line containing the pair of points. (−2,−6) and (−15,−7)

Answer 1

The linear regression for a given data set has the form

`y=a+bx`

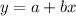
where the values a and b can be solved using the equation

`\begin{gathered} a=((\sum y)(\sum x^2)-(\sum x)(\sum xy))/(n(\sum x^2)-(\sum x)^2) \\ b=(n(\sum xy)-(\sum x)(\sum y))/(n(\sum x^2)-(\sum x)^2) \end{gathered}`

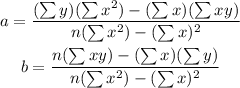
Based on the given data set, we have n equals 5. We will solve for the values of the summation first. We have the following

`\begin{gathered} \sum y=4+4+6+6+8=28 \\ \sum x=1+3+5+7+9=25 \\ \sum xy=(1\cdot4)+(3\cdot4)+(5\cdot6)+(7\cdot6)+(8\cdot9)=160 \\ \sum x^2=1^2+3^2+5^2+7^2+9^2=165^{} \\ (\sum x)^2=25^2=625 \end{gathered}`

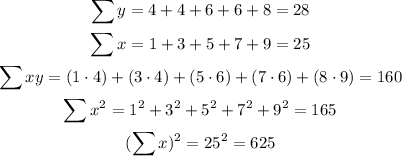
Using these values to compute for the values of a and b, we get

`\begin{gathered} a=((28\cdot165)-(25\cdot160))/(5(165)-625)=(31)/(10)=3.1 \\ b=(5(160)-(28\cdot25))/(5(165)-625)=(1)/(2)=0.5 \end{gathered}`

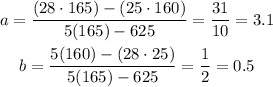
Take note that the problem wants us to reduce the numbers to the nearest tenth. Hence, the linear regression for the given data set is written as

`y=3.1+0.5x`