Question

A Tour de France cyclist at a rate of 6.5 m/s and is 333 m

ahead of a crew van with powerdrink refills. The van is
traveling at 15 m/s and is accelerating at a constant rate of
0.4 m/s2
How much time will it take for the crew van to catch up
with the cyclist?

Answer 1

Given data:

* The speed of the cyclist is 6.5 m/s.

* The initial distance of the cyclist from the van is 333 m.

* The initial velocity of the van is 15 m/s.

* The acceleration of the van is,

`a=0.4ms^(-2)`

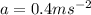
Solution:

Let x be the distance from the van initial position at which the cyclist and van meet.

Let the cyclist meet the van at time t.

By the kinematics equation, the position of the cyclist at time t is,

`x-333=u_ct+(1)/(2)a_ct^2`

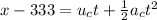
where u_c is the speed of the cyclist, a_c is the acceleration of the cyclist, t is the time taken and 333-x is the distance traveled by the cyclist at time t,

The acceleration of the cyclist is zero.

Substituting the known values,

`\begin{gathered} x-333=6.5t+0 \\ x-333=6.5t \end{gathered}`

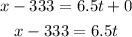
By the kinematics equation, the position of the van after time t is,

`x=u_vt+(1)/(2)a_vt^2`

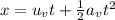
where u_v is the velocity of the van, a_v is the acceleration of the van, and t is the time taken,

Substituting the known values,

`\begin{gathered} x=15t+(1)/(2)*0.4* t^2 \\ x=15t+0.2t^2 \end{gathered}`

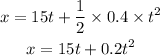
Substituting this value of x in the kinematics equation of the cyclist,

`\begin{gathered} (15t+0.2t^2)-333=6.5t \\ 15t+0.2t^2-6.5t-333=0 \\ 0.2t^2+8.5t-333=0 \end{gathered}`

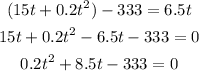
By solving the quadratic equation,

`\begin{gathered} t=\frac{-8.5\pm\sqrt[]{8.5^2-(4*0.2*(-333))}}{2*0.2} \\ t=\frac{-8.5\pm\sqrt[]{^{}8.5^2+(4*0.2*333)}}{2*0.2} \\ t=(-8.5\pm18.4)/(0.4) \\ t=24.8\text{ s or-67.25 s} \end{gathered}`

As the value of time cannot be negative.

Thus, the time at which the cyclist and van meet is 24.8 seconds.