Question

Number of adult tickets sold = Number of child tickets sold =

Answer 1

Given:

Total ticket = 321

Total collection = $3535

Adult ticket price = $15

Child ticket price = $5

Find-:

(1)

Number of adult tickets sold

(2)

Number of child tickets sold

Explanation-:

Let the number of adult tickets = x

Let the number of child tickets = y

If the total ticket is 321 then,

`x+y=321........................(1)`

Price for adult ticket is:

`=15x`

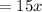
The price for child ticket is:

`=5y`

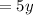
total price is $3535 then,

`15x+5y=3535...................(2)`

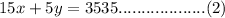
From eq(1)

`\begin{gathered} x+y=321 \\ \\ 5x+5y=1605..............(3) \end{gathered}`

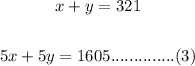
So eq(2) - eq(3) is:

`\begin{gathered} (15x+5y)-(5x+5y)=3535-1605 \\ \\ 15x-5x+5y-5y=1930 \\ \\ 15x-5x=1930 \\ \\ 10x=1930 \\ \\ x=(1930)/(10) \\ \\ x=193 \end{gathered}`

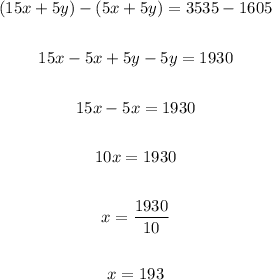
Put the value in eq(1) then,

`\begin{gathered} x+y=321 \\ \\ 193+y=321 \\ \\ y=321-193 \\ \\ y=128 \end{gathered}`

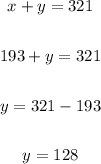
So,

Number of adult tickets = 193

Number of child tickets = 128