ANSWER:
(a) 4.73*10^-30 m
(b) 2.37*10^-19 times smaller
Explanation:
Given:
Mass of ball = m = 0.10 kg
Speed of ball = v = 1.4x10^-3 m/s
(a)
Since, de Broglie wavelength is given by:
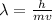
Where, h is the Plank's Constant ( h = 6.626x10^-34 kg m^2/s). Therefore, de Broglie wavelength of the ball will be:
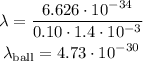
(b)

It means that the wavelength of the ball is 2.37*10^-19 times smaller