Solution:
Given the triangle ABC as shown below:
To draw the image,
step 1: Determine the coordinates of the vertices of the triangle.
In the above graph,
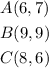
step 2: Evaluate the new coordinates A'B'C' of the triangle after a dilation centered at the origin with a scale factor of 2.
After a dilation centered at the origin with a scale factor of 2, the iniatial coordinates of the vertices of the triangle are multiplid by 2.
Thus,
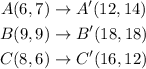
step 3: Draw the triangle A'B'C'.
The image of the triangle A'B'C' is as shown below: