The hole appears in the rational function when the numerator and the denominator have the same zeroes
Since the rational function is
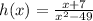
Factorize the denominator
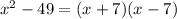
The rational function h(x) is
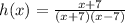
Since (x + 7) is in both numerator and denominator
Then there is a hole at x + 7 = 0
Let us find the value of x
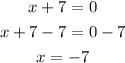
The whole is at x = -7
Then simplify the fraction to find the value of y at x = -7
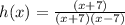
Cancel the bracket (x+7) up by the same bracket down
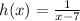
Substitute x by -7
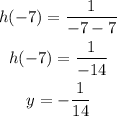
The hole is at (-7, -1/14)