We need to find the area of Shape C.
Please have a look at the diagram below:
To find x, we can use the Pythagorean Theorem on the right triangle.

Now, let's solve for x. The steps are shown below:
![\begin{gathered} 100^2+x^2=107^2 \\ x^2=107^2-100^2 \\ x^2=11449-10000 \\ x^2=1449 \\ x=\sqrt[]{1449} \\ x=38.07 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jasd6l9ca6baf9v47ze0091eiq2dn5ch6t.png)
So, the top part (dotted line) is
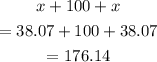
Now, we have a trapezoid. Let's find the area of the trapezoid:

Now, we need to subtract the area labeled (K) from the area of the trapezoid found.
--------------------------------------------------------------------------------
Area k is a triangle with side lengths 117, 117, and 176.14. Let's find the area of the triangle. The diagram is shown below:
Now, we will find h, the height of the triangle using Pythagorean Theorem.
![\begin{gathered} 88.07^2+h^2=117^2 \\ h^2=117^2-88.07^2 \\ h^2=5932.6751 \\ h=\sqrt[]{5932.6751} \\ h=77.02 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dt0g8l31rqru12fwfwgrydrslzh00fsepa.png)
The area of the triangle (region K) is,
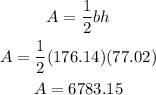
The area of region C is the area of trapezoid - area of region k (triangle). So, the area is >>>>
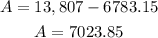
Answer7023.85