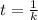The derivative is the instantaneous rate of change of a function with respect to one of its variables. This is equivalent to finding the slope of the tangent line to the function at a point.
The function is given to be:

where A and k are positive constants.
We can find the derivative of the function as follows:
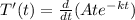
Step 1: Pull out the constant factor
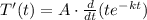
Step 2: Apply the product rule

Let

Therefore, we have:
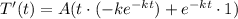
Step 3: Simplify

QUESTION A
At t = 0, the instantaneous rate of change is calculated to be:
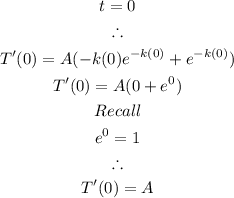
The rate of change is:
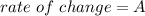
QUESTION B
At t = 30, the instantaneous rate of change is calculated to be:
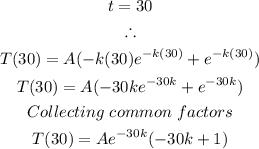
The rate of change is:
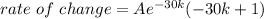
QUESTION C
When the rate of change is equal to 0, we have:
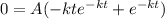
We can make t the subject of the formula using the following steps:
Step 1: Apply the Zero Factor principle

Step 2: Collect common terms

Step 3: Apply the Zero Factor Principle:
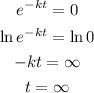
or
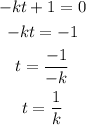
The time will be: