Question

PLEASE READ BEFORE ANSWERING: ITS ALL ONE QUESTION HENCE "QUESTION 6" THEY ARE NOT INDIVIDUALLY DIFFERENT QUESTIONS.

Answer 1

First, lets note that the given functions are polynomials of degree 2. Since the domain of a polynomial is the entire set of real numbers, the domain for all cases is:

`(-\infty,\infty)`

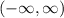
Now, lets find the range for all cases. In this regard, we will use the first derivative criteria in order to obtain the minimum (or maximim) point.

case 1)

In the first case, we have

`\begin{gathered} 1)\text{ }(d)/(dx)f(x)=6x+6=0 \\ which\text{ gives} \\ x=-1 \end{gathered}`

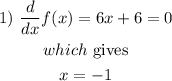
which corresponds to the point (-1,-8). Then the minimum y-value is -8 because the leading coefficient is positive, which means that the curve opens upwards. So the range is

`\lbrack-8,\infty)`

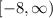
On the other hand, the horizontal intercept (or x-intercept) is the value of the variable x when the function value is zero, that is,

`3x^2+6x-5=0`

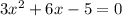
which gives

`\begin{gathered} x_1=-1+(2√(6))/(3) \\ and \\ x_2=-1-(2√(6))/(3) \end{gathered}`

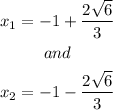
Case 2)

In this case, the first derivative criteria give us

`\begin{gathered} (d)/(dx)g(x)=2x+2=0 \\ then \\ x=-1 \end{gathered}`

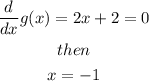
Since the leading coefficient is positive, the curve opens upwards so the point (-1,5) is the minimum values. Then, the range is

`\lbrack5,\infty)`
`\lbrack5,\infty)`

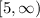
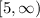
and the horizontal intercepts do not exists.

Case 3)

In this case, the first derivative criteris gives

`\begin{gathered} (d)/(dx)f(x)=-2x=0 \\ then \\ x=0 \end{gathered}`

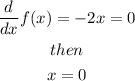
Since the leading coeffcient is negative the curve opens downwards and the maximum point is (0,9). So the range is

`(-\infty,9\rbrack`

and the horizontal intercepts occur at

`\begin{gathered} -x^2+9=0 \\ then \\ x=\pm3 \end{gathered}`

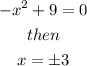
Case 4)

In this case, the first derivative yields

`\begin{gathered} (d)/(dx)p(t)=6t-12=0 \\ so \\ t=2 \end{gathered}`

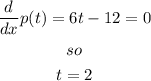
since the leading coefficient is postive the curve opens upwards and the point (2,-12) is the minimum point. Then the range is

`\lbrack-12,\infty)`

and the horizontal intercetps ocurr when

`\begin{gathered} 3x^2-12x=0 \\ which\text{ gives} \\ x=4 \\ and \\ x=0 \end{gathered}`

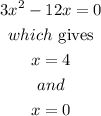
Case 5)

In this case, the leading coefficient is positive so the curve opens upwards and the minimum point ocurrs at x=0. Therefore, the range is

`\lbrack0,\infty)`

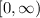
and thehorizontal intercept is ('0,0).

In summary, by rounding to the nearest tenth, the answers are: