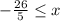Question

`( - 2 / 5) \leqslant (x + 4) / 3 \ \textless \ x + 5`solve the inequalities

Answer 1

We will solve this problem first, by solving the inequality in the left hand side and next the inequality on the right hand side.

In the left hand side, we have

`-(2)/(5)\le(x+4)/(3)`

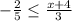
If we move 3 to the left hand side, we obtain

`-(2)/(5)\cdot3\le x+4`

which is equal to

`-(6)/(5)\le x+4`

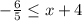
Now, if we move 4 to the left hand side as -4, we have

`\begin{gathered} -(6)/(5)-4\le x \\ -(6)/(5)-(20)/(5)\le x \\ (-6-20)/(5)\le x \\ -(26)/(5)\le x \end{gathered}`

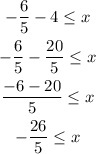
Now, in the right hand side, we have

`(x+4)/(3)and if we move 3 to the right hand side, we obtain[tex]x+4<3(x+5)`

we must note that, since 3 is positive, it doesnt flipt the inequality sign. Then, we obtain

`x+4<3x+15`

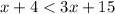
Now, if we move x to the right hand side we have

`\begin{gathered} 4<3x-x+15 \\ 4<2x+15 \end{gathered}`

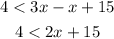
and finally, we have

and

`(-11)/(2)<p></p><p>and we must choose one of them. We can see that</p>[tex]\begin{gathered} -(11)/(2)<-(26)/(5) \\ \text{because} \\ -5.5<-5.2 \end{gathered}`

Therefore, the answer which fulfil both conditions is

`-(26)/(5)\le x`